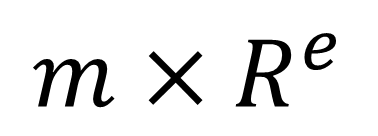指数表記
非常に大きい数
・20000000000000
また、非常に小さい数
・-0.000000000000385
などはゼロがたくさん並んでいます。このような場合によく使われるのが「指数表記」です。
先ほどの数字を指数表記にすると、
・2×1013
・-3.85×10-14
などと書くことができます。
指数表記を使うと、ゼロの数が減るだけではなく、数値の比較をしやすくなる特徴があります。
例えば、0.0000000000000000016と、0.00000000000000000091という数字を見てください。
このままではどちらが大きいかわかりにくいです。
しかし、指数表記にすると
1.6×10−18
9.1×10−19
となり、比較が簡単です。
指数表記には以下のような書き方のルールがあります。
ここで出てくる文字の意味は以下の通りです。
・Rは基数を表します
・mは仮数部と呼びます
仮数部は整数+小数の形にします
・eを指数部と呼びます
指数部は必ず整数です
・+やーなどの符号は先頭に付けます
指数表記への変換
123.456(10)という数字の指数表記を考えてみましょう。
基数が10なので、10倍すると数値が一けた大きくなり、小数点の位置が右に移動します。
123.456×10 → 1234.56
10倍しただけだと数値が変わってしまうので、元の数値に戻すために10-1倍します。
123.456
=(123.456×10) ×10-1
=1234.56×10-1
100倍、つまり102倍の時も同様です。
123.456
=(123.456×102) ×10-2
=12345.6×10-2
逆に10で割る、つまり10-1 倍すると数値が一けた小さくなり、小数点の位置が左に移動します。
123.456×10-1 → 12.3456
10-1倍しただけだと数値が変わってしまうので、元の数値に戻すために101倍します。
123.456
=(123.456×10-1) ×101
=12.3456×101
2進数の指数表記
数字が2進数になった場合も10進数の場合と同じように考えます。
ただし、基数は「2」です。
2倍すると数値が一けた大きくなり、小数点の位置は右に移動します。
110.11
=1101.1×2-1
=11011×2-2
2-1倍すると数値が一けた小さくなり小数点の位置は左に移動します。
110.11
=11.011×21
=1.1011×22
次は指数表記の正規化を練習しましょう